Introduction
Hi, my name is Kubo, welcome to my home page.
- I used to work at fb.
- I have done a phd in bioinformatics (Algorithms for Genome Rearrangements).
- I am interested in algorithm visualization.
Contact: jakub [dot] kovac47 [at-sign] gmail.com
CV: pdf
Teaching
Selected Topics in Data Structures at Comenius University.
At Comenius University.
Visualizations
Gnarley trees is a project focused on visualization of various tree data structures. It contains dozens of data structures, from balanced trees and priority queues to union find and stringology.
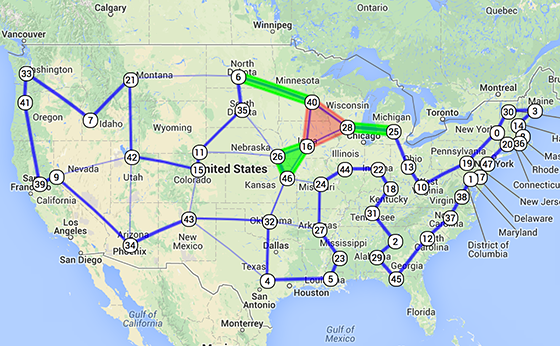
What is the shortest path going through a given set of cities? This visualization shows various heuristics (nearest neighbour, 2-opt) and also an exact method using linear programming.
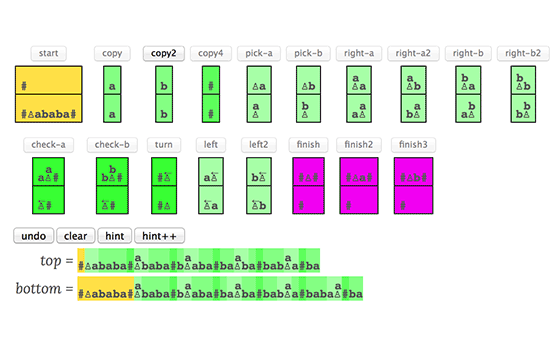
PCP is a simple-looking puzzle involving domino-like tiles which we should put together so that the words spelled out on the top and bottom are the same. Well, it turns out that this puzzle is much much harder than it seems...
Fibonacci, Tribonacci, and Matrices
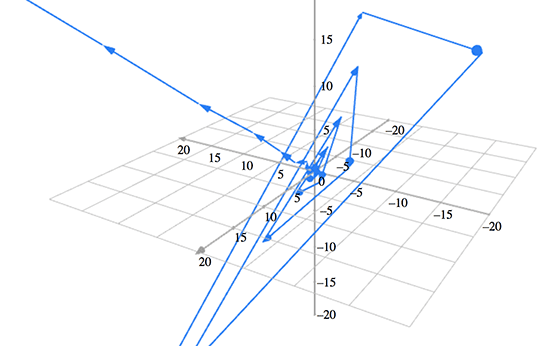
Fibonacci numbers is a sequence 1, 1, 2, 3, 5, 8, 13, 21, ... where each term is a sum of previous two terms (Fn=Fn-1+Fn-2). Tribonacci sequence is a variation, where each term is a sum of previous three terms (1, 1, 2, 4, 7, 13, 24, ...). One way to analyze Fibonacci and Tribonacci numbers is to consider a sequence of points in 2D (Fk+1, Fk) or in 3D (Tk+2, Tk+1, Tk) and analyze the linear transformations producing the sequences (and their eigenvalues; see wiki).
Words in different languages
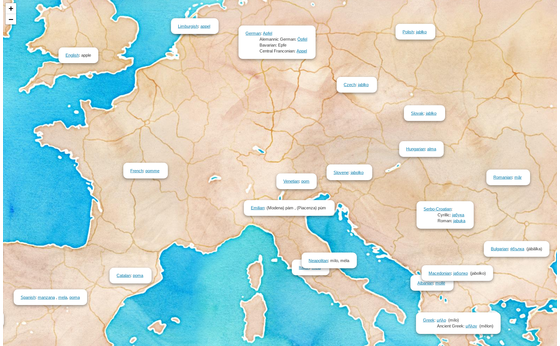
An interactive map showing how to say a word in different languages. For example the word apple comes from Proto-Indo-European *ab(e)l- (and is thus related to Dutch: appel, Old Norse eple, or German Apfel), while in Slavic languages, it is related to Proto-Slavic *ablъko (Slovak jablko, Russian я́блоко (jábloko), Croatian jabuka), while in other languages, this word is derived from Ancient Greek μῆλον (mêlon) (which also meant fruit in general), Latin pomum, or Proto-Turkic alma.
Have fun and try different words (e.g. grass, life, or computer).
On cubes and pyramids
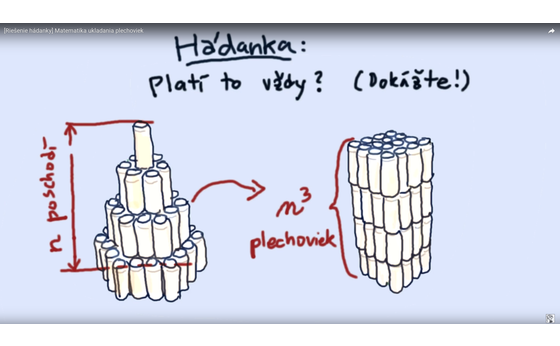
Grab a couple of cans and build a hexagonal pyramid. Now build a cube of the same height. You'll discover you needed the same number of cans! Is it true for any height? Why? (A puzzle by matikaza3minuty.)
Here is my answer showing how a pyramid can be continuously transformed into a cube and vice versa. This shows a correspondence between pyramid floors and layers of a cube and yields a proof by induction.
Expositions (in Slovak)
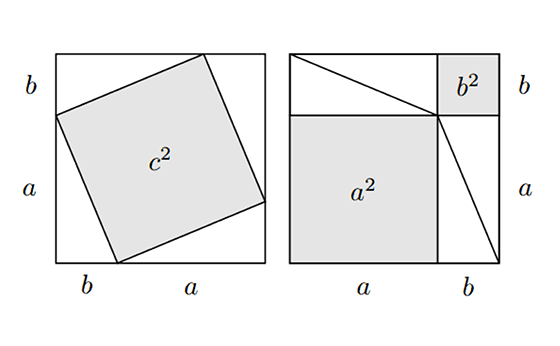
Pytagorovu vetu sa učia "recitovať" deti na celom svete. Vedeli by ste ju aj dokázať? A viete, na čo je to vlastne dobré vedieť?
Jedna z vecí, čo robí matematiku ťažko pochopiteľnou, je abstrakcia. My si naopak ukážeme príklady, kde nám väčšia abstrakcia môže pomôcť, veci zjednodušiť, alebo ukázať súvislosti medzi oblasťami, ktoré zdanlivo vôbec nesúvisia. Čo má spoločné Pytagoras a Hippokrates? Zmena súradnicovej sústavy, Fourierova transformácia a JPEG? Čínska zvyšková veta a interpolácia? A ako spočítame uhol medzi dvoma článkami? Možno sa to dozvieme, ak sa na veci pozrieme trochu abstraktnejšie.
V roku 1994 vyvolalo veľký rozruch nájdenie sekvencie dinosaurej DNA. Čo všetko sme sa z toho dozvedeli? Čo všetko sa vôbec môžeme z takej DNA dozvedieť? Bude onedlho Jurský park skutočnosťou?
Uverejnené v časopise .týždeň 20. marca; číslo 12/2010